What is the relevance of n‑Value in superconductivity?

If you come to superconductivity from a general physics or engineering background, one concept tends to feel oddly under‑explained: the n‑value. It’s not part of the classic London equations. It doesn’t appear in BCS theory. And yet, if you talk to anyone designing superconducting magnets, power cables, or fusion devices, n‑value suddenly becomes critically important. So, what exactly is the n‑value, and why does it matter so much in practice?

The short answer is that the n‑value is the bridge between ideal superconducting physics and the messy reality of real materials and real systems.

From Ohm’s law to the London equations

Most engineers are familiar with Ohm’s law:

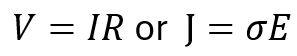
It tells us that current responds linearly to an applied electric field, with energy dissipated as heat. This framework breaks down completely for superconductors, because their resistance is (by definition) zero.

To replace Ohm’s law, Fritz and Heinz London introduced the London equations in 1935. Rather than linking current to voltage, they relate current to electromagnetic fields:

• The first London equation says that an electric field causes the supercurrent to accelerate, not merely flow.
• The second London equation explains the Meissner effect: magnetic fields are expelled from the interior of a superconductor.

In this ideal picture, superconductors have:

• zero dissipation,
• persistent currents,
• perfect diamagnetism.

This is beautiful physics, but it’s also too perfect.

Real superconductors are not binary switches

In an ideal world, a superconductor would behave like a vertical step function:

• Zero voltage up to the critical current J_c
• Sudden failure beyond it

But real superconductors, especially Type‑II materials used in magnets, power cables, and fusion devices, do not behave this way.

Instead, as current approaches J_c, tiny but measurable electric fields begin to appear. The material is still “superconducting” in a practical sense, but it is no longer perfectly lossless.

This gradual transition is where the n‑value enters the story.

The Power Law and the meaning of n

In engineering practice, superconductors are often described using an E–J power law:

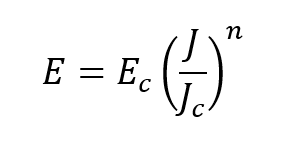
Here:

• E_c is a small reference electric field (often 1 µV/cm),
• J_c is the critical current density,
• n determines how sharp or broad the transition is.

Intuitively:

• High n‑value (≈ 30–100):
  A very sharp transition. The conductor behaves almost ideally until it suddenly becomes resistive.
• Low n‑value (≈ 10–20):
  A broad, “leaky” transition. Resistance and heating creep in well before full loss of superconductivity.

This is why n‑value is often called a quality index for superconducting materials.

What determines the n‑Value?

At the microscopic level, n‑value is closely linked to flux creep.

In Type‑II superconductors, magnetic flux penetrates the material in quantised vortices. These vortices are pinned by defects in the crystal structure. Under high current or temperature, they can thermally hop between pinning sites, producing small electric fields.

From this perspective:

• High n‑values imply strong, uniform flux pinning.
• Low n‑values often indicate material inhomogeneity, defects, or uneven current distribution.

So, while J_c tells you how much current a conductor can carry, n‑value tells you how cleanly it does so.

There are 4 key reasons why engineers care so much about n‑Value

1. Magnet stability

In applications like MRI, NMR, and fusion magnets, persistent current stability is crucial. a high n-value is critical to ensure the current doesn’t decay over time due to tiny “leaks” in the superconducting state.

2. Quench detection and protection

A quench is the sudden transition from superconducting to normal resistive behaviour. It can be violent and destructive if not managed correctly. Knowing the n‑value helps engineers predict a quench, the point at which a superconductor heats up and transitions to a normal, resistive state. A high n-value means less warning before a quench happens. A low n‑value means more gradual heating, but higher losses during normal operation.

Knowing the n‑value is essential for designing quench protection systems.

3. Numerical modelling and simulation

This is one of the most under‑appreciated roles of n‑value.

The London equations assume exactly zero resistivity. Unfortunately, this causes serious problems for numerical solvers used in finite‑element modelling:

• Zero resistivity leads to mathematical singularities.
• Fault and transient simulations become impossible.

The power law, with its n‑value, provides a solution by introducing a non‑linear, current‑dependent resistivity:

---

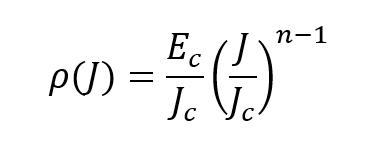
This “pseudo‑resistivity” is:

• extremely small at low currents,
• rapidly increasing near J_c ,
• continuous and differentiable.

That makes it compatible with standard formulations of Maxwell’s equations used in power grid, magnet, and cable simulations.

4. Modelling failure and faults

Crucially, the London equations only describe the superconducting state. They cannot describe what happens after failure begins. The power law can.

This makes n‑value indispensable for:

• modelling quenches,
• designing superconducting fault current limiters (SFCLs),
• simulating grid‑scale disturbances in HTS power systems.
  

So, the n‑Value is of great practical importance.

The London equations tell us what superconductivity is.

The critical current tells us how far we can push a material.

The n‑value tells us how superconductivity fails and how safely we can operate near the limit.

In other words, the n‑value is not fundamental physics in the same sense as the London equations, but it is absolutely fundamental in making superconductivity work in the real world.

And that’s why, whether you’re designing fusion magnets, power cables, or aviation systems, the humble n‑value ends up carrying far more weight than its simple definition might suggest.